Over the coming weeks and months, expect to hear statistics such as the following:
"Over 43% of Covid-19 deaths in England have been in adults who were fully vaccinated against the disease."
"About half of all adults infected in an outbreak of the Delta variant in Israel were fully inoculated with the Pfizer vaccine."
While neither of these is inaccurate, they are certainly misleading in that they lead the reader to come to the conclusion that the Covid vaccines are not working effectively, hospitalisations and deaths are not going to be prevented in the future, the sky is falling etc. etc. To assuage anyone of this notion, we can in fact be assured that the vaccines are still working incredibly well even against the Delta variant. A recent comprehensive real-world study from Public Health England revealed that two doses of the vaccine are 96% effective against hospitalisation, actually more effective than they are against the Alpha variant in point estimate terms – the confidence intervals overlap so it is more accurate to say it is no less effective against the new dominant variant. There appears to be some vaccine escape when it comes to infection, however, as two doses are estimated to be 79% effective at preventing symptomatic Covid for Delta vs 89% for Alpha. As a slight aside, this is obviously a slight annoyance but is not a major issue as the systemic problems that this virus has caused have been due to its propensity to put people in hospital and, unfortunately, to cause deaths. As long as the vaccines are remaining effective against hospitalisations and deaths, there is really nothing to worry about even if the number of cases does reach a high number.
If the vaccines still remain effective, how can these statistics still emerge? The reason is subtle, and perhaps counter-intuitive, but is due to the base rate fallacy and our trusty old friend Bayes' rule. The base rate fallacy essentially tells us that when we look at the percentage of event X that occurs in groups A, B, C, etc., we have to consider the fraction of the population which each of these groups comprises in the overall population (the base rate) in order to know the correct conditional probability of event X happening to a member of a given group. In this case, the event is being infected with Covid and the groups are people who are vaccinated fully, partially vaccinated and unvaccinated against the virus. The crucial thing to realise here is that the probability of getting Covid given that someone is fully vaccinated differs substantially from the probability that someone is fully vaccinated given that they have got Covid. This is not something that people find easy to appreciate intuitively and forms a bias in processing information of this kind. Let's look at two well-known examples that clearly illustrate the base rate fallacy, the first more trivial and the second less so.
Suppose I tell you that 90% of crime is committed by people who are right-handed. Naively, you may conclude that right-handed people have some kind of predisposition to breaking the law and as such should probably be subject to government intervention to address this. Of course, most people would correctly realise this is complete nonsense. If right- and left-handed people are equally likely to commit a crime, right-handers make up 90% of the population and 1% of the whole population commit a crime, we can apply Bayes rule to tell us the probability that someone commits a crime (C) given that they are right-handed (R):
I.e. the probability that someone commits a crime given that they are right-handed is 1%, which is exactly equal to the probability that anyone, regardless of their dominant hand, commits a crime. Note that Pr(X|Y) means the probability of X happening given that we know Y – a conditional probability. You can redo the calculations and find that the analogous probability for left-handers is also 1%, and as a result, knowing a person's handedness does not cause us to update our posterior probability that they are a criminal.
As a second example which comes from Kahneman and Taversky, suppose you have the task of guessing what degree someone studied at university after being told a number of their characteristics. You are informed that the person is male, has a passion for video games and loves coding. What subject would you guess? I imagine there is a reasonable chance your guess was computer science, and indeed around 95% of respondents said it was more likely that the person was studying computer science than a humanities subject. This is, however, once again incorrect reasoning because the respondents were ignoring the base rates of each group in the overall population and overweighting the idiosyncratic information. Far more students are enrolled in humanities courses than in computer science degrees, making this a more likely option even if the listed characteristics are highly correlated with studying the latter.
Now let's return to the Covid example. Hopefully, you will now appreciate that in order to evaluate the probability that someone gets infected with Covid (C) given they are fully vaccinated (FV) depends on the fraction of the population that are fully vaccinated and the efficacy against infection that being fully vaccinated gives. Using Public Health England data, we know that of the 9571 Delta cases which were found in the over 50s population, 3546 (37%) of these were in people who were fully vaccinated. We also know that as of June 20th, 92% of all over 50s have been fully vaccinated but we will bump this down a bit to 88% since the time span for the cases stems from May to June and so the average vaccination rate over this period will be lower than its endpoint. Finally, let's assume that of the remaining 12%, just under half of these were unvaccinated (UV) completely so 5%. Of the 9571 Delta cases, 976 (10%) were in the unvaccinated contingent. We can now calculate a crude estimate of vaccine efficacy against symptomatic Covid from the Delta variant by using Bayes' rule:
We now divide the two to get rid of the Pr(C) term and to give us the fully vaccinated efficacy estimate:
I.e. the risk of getting Covid when fully vaccinated is 21% of what it is when unvaccinated, and the vaccine is 79% effective which matches the Public Health England estimate. So even though a relatively high fraction of over 50s cases were in the fully vaccinated population, the vaccine is still highly effective.
Unfortunately, as the percentage of the population who are fully vaccinated increases, this problem only gets worse as an increasing fraction of cases will be amongst the fully vaccinated. If 100% of the population were fully vaccinated then 100% of all cases would be amongst the fully vaccinated, no matter the rate of vaccine efficacy! The graph below illustrates this using the real-world estimate of vaccine efficacy and the vertical line denoting the fraction of the population we have currently fully vaccinated. This serves to highlight that the relationship is actually non-linear, as after we have fully vaccinated around 60% of the population the fraction of cases in the fully vaccinated starts to rise very sharply.
As I have alluded to previously, many people seem to have a large demand for bad Covid news and I imagine that statistics guilty of the base rate fallacy will be pushed by media outlets as a way of fulfilling this. A factor that compounds the issue is the mortality profile of the virus, which skews overwhelmingly towards the over 50s who are also far more likely to be fully vaccinated than the younger age groups. Pre-vaccine, around 99% of all Covid deaths were among this group and this will not change post-vaccine, although crucially the number of deaths will be dramatically lowered. Consequently, we would already expect a very large fraction of deaths to be amongst the fully vaccinated, and it is absolutely no cause for alarm.


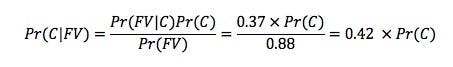
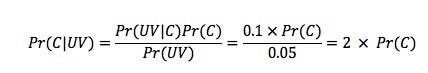


Well, this aged badly.