Why Does the Last Leg of Accumulator Bets Let People Down So Often?
Probability is tricky unless you are guided by the good Reverend Bayes
Probability can be infamously counterintuitive. The most famous example of this is the classic Monty Hall problem, which goes as follows: suppose you are on a game show and the host shows you three doors. Behind two of these doors, you will find a goat. Behind the other, there is a brand new sports car. Your task is to win the car by guessing the correct door. You make the first guess by selecting a particular door, but then the host opens one of the other two doors that you did not guess to reveal a goat. He then gives you the option to change your guess or stick with your original one — what should you do? Intuitively, many people feel that the revelation of this new piece of information by the host effectively turns the game into a 50/50 proposition, meaning that there should be no advantage to changing your guess. This is, however, incorrect, as it is actually optimal to change your guess after the host gives you the opportunity to do so. For example, suppose you initially pick door A and then the host shows you that there is a goat behind door B, it is in your best interest to switch your guess to door C. It turns out that switching your guess means you will win the car 2/3 of the time, while if you stick with your original guess you will only win 1/3 of the time.
If you find this hard to wrap your head around, you are in good company. The problem became well-known after it was sent in by a reader to Marilyn vos Savant, who wrote a column for Parade magazine, in 1990. For context, Vos Savant is the owner of the highest ever recorded IQ as verified by the Guinness Book of World Records. In her response to the problem, she correctly posited that the optimal strategy was to switch your guess. This led to a barrage of letters, over 10,000 of them in fact, from readers who were convinced she was wrong. 1,000 of these were from people with a PhD, and even the legendary mathematician Paul Erdos was initially skeptical before changing his mind after seeing simulations of each strategy. This extract from a letter by Scott Smith, the holder of a PhD from the University of Florida, is too good to not include:
You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I'll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don't need the world's highest IQ propagating more. Shame!
One way to understand the Monty Hall problem is to apply Bayes’ rule:
P(A|B) is the probability of event A happening given we know that event B has happened. P(A) and P(B) are the respective unconditional probabilities of events A and B. For example, the unconditional probability of someone becoming a professional footballer is very low. However, the probability of someone becoming a professional footballer given they are a member of Chelsea’s academy is much higher. In the language of Bayes, P(A) is our prior probability of A happening, and P(B|A) is the likelihood of B happening given A.
Suppose we guess that the car is behind door A, and then the host opens door B to reveal a goat. In our case, A represents the car being behind door A, and B represents the host opening door B to show a goat behind there. We can start by calculating our prior, P(A). Given that before the game started, one out of the three doors contained a car, it must then be the case that P(A) = 1/3. We then move on to the likelihood, P(B|A), which represents the probability that the host would open door B given that the car is behind door A. If the car is indeed behind door A, this means the host could either open door B or door C, and they randomise over each of these with equal probability which yields P(B|A) = 1/2. We now only have P(B) left to compute. This is the probability that the host opens door B. Again, the host only has two doors he could have opened and so P(B) = 1/2. Putting all this together gives P(A|B) = (1/3)*(1/2)/(1/6) = 1/3. We can repeat the calculations for P(C|B) — the probability that the car is behind door C given that we have guessed A and the host has opened B — and find that this is equal to 2/3, verifying that it is indeed better to switch our guess to door C. See here for the calculations. We could have alternatively observed that the door has to be behind either door A or door C, meaning that P(A|B) + P(C|B) = 1 and so P(C|B) must be 2/3.
This is a very well-known probability puzzle, but I will now outline a less well-known one — the case of the last leg of an accumulator seeming to frequently let a gambler down. For those who are not familiar with this term, an accumulator (parlay in American parlance) is where you bet that multiple events (legs) will all happen. I.e. Man Utd will lose to Brentford and Man City will beat Bournemouth. You need to guess all legs of the accumulator correctly in order to win the bet. For simplicity, let’s assume that a gambler has put down a 2-leg accumulator on two games that are being played at the same time, and each leg of the accumulator has a 1/2 probability of being correct. Suppose I tell you that at least 1 of the 2 legs is correct and then pose the question: what is the probability of both legs being correct and the accumulator winning? Intuition would tell you that it would be 1/2 since it has essentially come down to the last leg which has a 50/50 chance of winning. Just like the Monty Hall problem, intuition leads one astray here.
In this case, A now represents both of the two legs being guessed correctly and B represents at least 1 leg being guessed correctly. We can start with our prior once again, P(A). Each leg has a 50% chance of being correct and so the unconditional probability of getting both correct (assuming independence) is (1/2)^2 = 1/4. We can then move onto the likelihood, P(B|A), i.e. the probability of getting at least 1 leg correct given that we have guessed both correctly. This is clearly equal to 1 since if we get both legs right we have by definition got at least one correct. Finally, we need to calculate P(B) which is the probability of getting at least one leg correct. This can either happen if we guess one correctly, or if we guess both correctly, meaning we add these two probabilities: 1/2 + (1/2)^2 = 3/4. Putting everything together we get that P(A|B) = (1/4)/(3/4) = 1/3, and so the probability of winning the accumulator given that we have got one leg correct is one-third, and not one-half as we would intuitively have thought. So gamblers having their heart broken by the last leg of their accumulator is more common than you might imagine given your intuition.
It actually gets even weirder when you increase the number of legs in the accumulator. Suppose there is a 1000-leg accumulator and I tell you at least 999 of the legs have been guessed correctly, the probability of the accumulator winning is a mere 1/1000 — very far away from our 50/50 intuition!
A general lesson here is that people do not find conditional probability to be particularly intuitive. While in the case of accumulators it is rather inconsequential besides causing the gambler to feel unluckier than they really should, in other cases it can be more problematic. In July last year, I wrote about how the base rate fallacy would likely cause people to wildly misunderstand Covid statistics. Indeed, I was rather vindicated as the statistic of the following format was regularly peddled around:
x% of Covid-19 deaths have occurred in people who are fully vaccinated
This unfortunately led some to believe that the vaccines are far less effective in preventing mortality than they actually are. A personal irritant of mine is the tendency of others to preach that pretty much everything that is really just basic common sense should be taught in schools, given how little the average student retains from their education. However, teaching probability more in schools is something that I do think has a fair amount of merit, precisely because it can often deviate from common sense logic in quite meaningful ways as I have illustrated above.
Things I Have Enjoyed Recently
Car seats as contraception. “Since 1977, U.S. states have passed laws steadily raising the age for which a child must ride in a car safety seat. These laws significantly raise the cost of having a third child, as many regular-sized cars cannot fit three child seats in the back. Using census data and state-year variation in laws, we estimate that when women have two children of ages requiring mandated car seats, they have a lower annual probability of giving birth by 0.73 percentage points. Consistent with a causal channel, this effect is limited to third child births, is concentrated in households with access to a car, and is larger when a male is present (when both front seats are likely to be occupied). We estimate that these laws prevented only 57 car crash fatalities of children nationwide in 2017. Simultaneously, they led to a permanent reduction of approximately 8,000 births in the same year, and 145,000 fewer births since 1980, with 90% of this decline being since 2000.“
You may have noticed that I have finally given this blog a name. It comes from this splendid quote from John Maynard Keynes which I think many could do with hearing in our current climate: “Words ought to be a little wild, for they are the assaults of thoughts on the unthinking.“
The US is staggeringly over-imprisoned and under-policed:
This paper finds that cutting corporation tax leads to a long-run increase in real GDP. Particularly relevant given the Truss campaign’s promise to do just this. I personally think there are other effective things that could be done with corporation tax beyond the headline rate, such as moving to full expensing. Some other good ideas here.
Further to this point, we need a fundamental re-think of taxation in general due to the shift towards an ideas-based economy. Great paper on this by Chad Jones. The calls to simply ‘tax the rich’ will make all of us poorer. “This paper considers the taxation of top incomes when the following conditions apply: (i) new ideas drive economic growth, (ii) the reward for creating a successful innovation is a top income (though people can earn high incomes in other ways as well), and (iii) innovation cannot be perfectly targeted by a separate research subsidy — think about the business methods of Walmart, the creation of Uber, or the “idea” of Amazon. These conditions lead to a new force affecting the optimal top tax rate: by slowing the creation of new ideas that raise aggregate GDP, top income taxation reduces everyone’s income, not just the income at the top. When the creation of ideas is the ultimate source of economic growth, this force sharply constrains both revenue-maximizing and welfare-maximizing top tax rates.“
Just like the stars of big budgets films, CEOs are also getting older. There are now only two CEOs of S&P 500 companies who are under the age of 40. And we wonder why the UK and US economies lack dynamism…
A wonderful piece about walking around London, something I think is highly underrated.
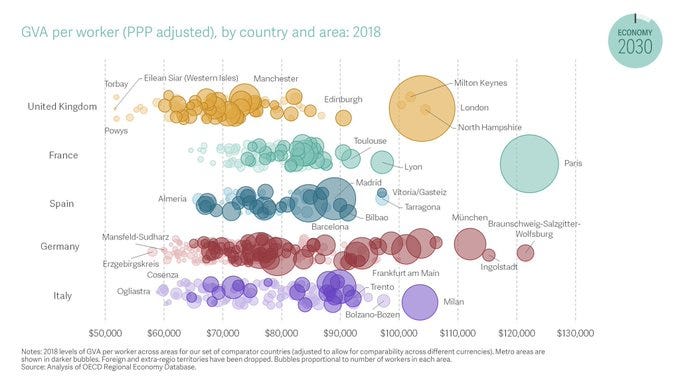
The poorest parts of the UK are poorer than the poorer parts of France, Germany, Spain and Italy:
Also, the gap between London + the South East and the rest of the UK is almost comical: